Practical 7: Bayesian Hierarchical Modelling

VIBASS

Source: vignettes/p7.Rmd

Bayesian Hierarchical Modelling

In this last practical we will consider the analysis of Bayesian hierarchical models. As explained in the previous lecture, hierarchical models provide a convenient tool to define models so that the different sources of variation in the data are clearly identified. Bayesian inference for highly structured hierarchical models can be difficult and may require the use of Markov chain Monte Carlo methods.

However, packages such as BayesX and INLA, to mention just two, provide a very convenient way to fit and make inference about certain types of Bayesian hierarchical models. We will continue using BayesX, although you can try out using INLA if you look at the optional, additional material in Practical 8.

Linear Mixed Models

Linear mixed models were defined in the lecture as follows:

Yij=Xijβ+ϕi+ϵij Y_{ij} = X_{ij}\beta +\phi_i+\epsilon_{ij}

Here, Y_{ij} represents observation jj in group ii, X_{ij} are a vector of covariates with coefficients β\beta, ϕi\phi_i i.i.d. random effects and ϵij\epsilon_{ij} a Gaussian error term. The distribution of the random effects ϕi\phi_i is Gaussian with zero mean and precision τϕ\tau_{\phi}.

Multilevel Modelling

Multilevel models are a particular type of mixed-effects models in which observations are nested within groups, so that group effects are modelled using random effects. A typical example is that of students nested within classes.

For the next example, the nlschools data set (in package MASS) will be used. This data set records data about students’ performance (in particular, about a language score test) and other variables. The variables in this data set are:

  • lang, language score test.

  • IQ, verbal IQ.

  • class, class ID.

  • GS, class size as number of eighth-grade pupils recorded in the class.

  • SES, social-economic status of pupil’s family.

  • COMB, whether the pupils are taught in the multi-grade class with 7th-grade students.

The data set can be loaded and summarised as follows:

library("MASS")
data("nlschools")
summary(nlschools)
##       lang             IQ            class            GS             SES       
##  Min.   : 9.00   Min.   : 4.00   15580  :  33   Min.   :10.00   Min.   :10.00  
##  1st Qu.:35.00   1st Qu.:10.50   5480   :  31   1st Qu.:23.00   1st Qu.:20.00  
##  Median :42.00   Median :12.00   15980  :  31   Median :27.00   Median :27.00  
##  Mean   :40.93   Mean   :11.83   16180  :  31   Mean   :26.51   Mean   :27.81  
##  3rd Qu.:48.00   3rd Qu.:13.00   18380  :  31   3rd Qu.:31.00   3rd Qu.:35.00  
##  Max.   :58.00   Max.   :18.00   5580   :  30   Max.   :39.00   Max.   :50.00  
##                                  (Other):2100                                  
##  COMB    
##  0:1658  
##  1: 629  
##          
##          
##          
##          
##

The model to fit will take lang as the response variable and include IQ, GS, SES and COMB as covariates (i.e., fixed effects). This model can easily be fit with BayesX (using the R2BayesX package) as follows:

library("R2BayesX")
m1 <- bayesx(lang ~ IQ + GS +  SES + COMB, data = nlschools)

summary(m1)
## Call:
## bayesx(formula = lang ~ IQ + GS + SES + COMB, data = nlschools)
##  
## Fixed effects estimation results:
## 
## Parametric coefficients:
##                Mean      Sd    2.5%     50%   97.5%
## (Intercept)  9.7059  1.0630  7.6150  9.7073 11.7042
## IQ           2.3878  0.0723  2.2494  2.3892  2.5301
## GS          -0.0263  0.0246 -0.0735 -0.0261  0.0227
## SES          0.1483  0.0143  0.1195  0.1488  0.1754
## COMB1       -1.6901  0.3123 -2.3009 -1.6999 -1.0776
##  
## Scale estimate:
##           Mean      Sd    2.5%     50% 97.5%
## Sigma2 48.0652  1.4518 45.2863 48.0170 51.07
##  
## N = 2287  burnin = 2000  method = MCMC  family = gaussian  
## iterations = 12000  step = 10

Note that the previous model only includes fixed effects. The data set includes class as the class ID to which each student belongs. Class effects can have an impact on the performance of the students, with students in the same class performing similarly in the language test.

Very conveniently, Bayesx can include random effects in the model by adding a term in the right hand side of the formula that defined the model. Specifically, the term to add is sx(class, bs = "re") (see code below for the full model). This will create a random effect indexed over variable class and which is of type re, i.e., it provides random effects which are independent and identically distributed using a normal distribution with zero mean and precision τ\tau - there are clear similarities with a residual terms here (although that is at the observation level, rather than the group level).

Before fitting the model, the between-class variability can be explored by means of boxplots:

boxplot(lang ~ class, data = nlschools, las = 2)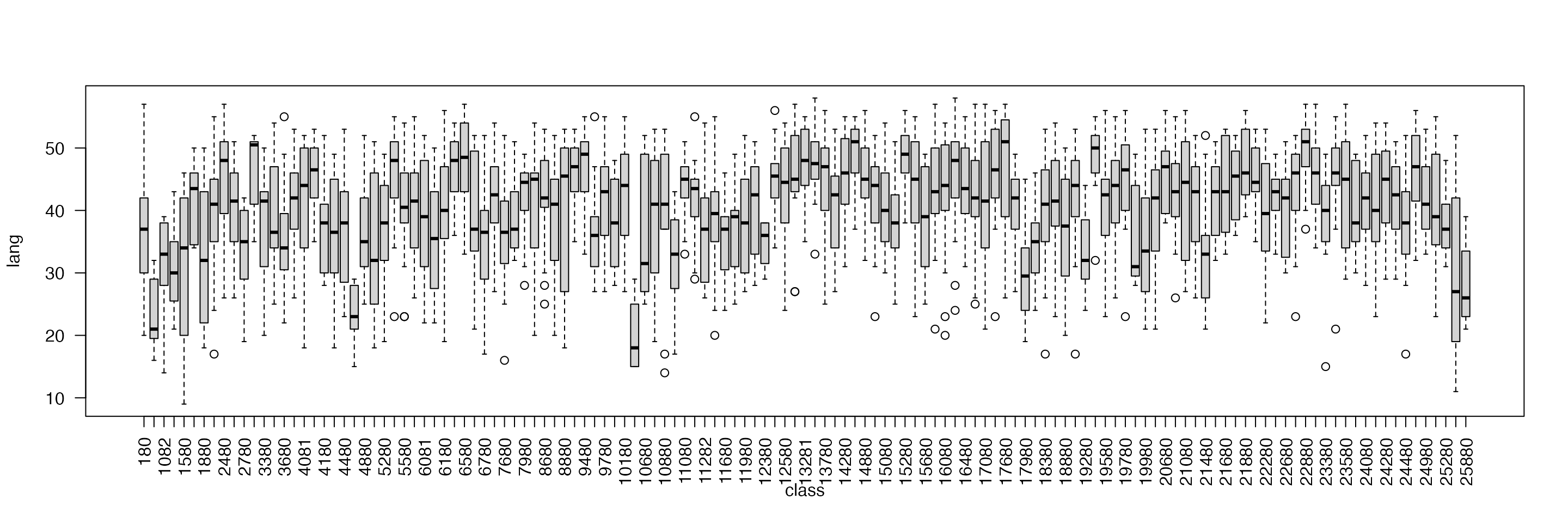

The code to fit the model with random effects is:

m2 <- bayesx(
  lang ~ IQ + GS +  SES + COMB + sx(class, bs = "re"),
  data = nlschools
)

summary(m2)
## Call:
## bayesx(formula = lang ~ IQ + GS + SES + COMB + sx(class, bs = "re"), 
##     data = nlschools)
##  
## Fixed effects estimation results:
## 
## Parametric coefficients:
##                Mean      Sd    2.5%     50%   97.5%
## (Intercept) 10.6158  1.4532  7.8300 10.5345 13.5842
## IQ           2.2460  0.0749  2.1000  2.2481  2.3950
## GS          -0.0154  0.0477 -0.1069 -0.0162  0.0746
## SES          0.1652  0.0149  0.1359  0.1653  0.1966
## COMB1       -1.9744  0.5852 -3.1245 -1.9681 -0.8178
##  
## Random effects variances:
##                 Mean      Sd    2.5%     50%   97.5%     Min    Max
## sx(class):re  8.6044  1.3576  6.1081  8.5338 11.4041  5.0351 14.372
##  
## Scale estimate:
##           Mean      Sd    2.5%     50%  97.5%
## Sigma2 40.0422  1.1947 37.7744 40.0373 42.308
##  
## N = 2287  burnin = 2000  method = MCMC  family = gaussian  
## iterations = 12000  step = 10

You can compare this Bayesian fit with a non-Bayesian analysis, this time making use of the lmer()' function in the packagelme4. (Here,lmemeanslinear effects.) We present the code only for comparison, and we do not describe lmer() or lme4 more fully.

## Loading required package: Matrix
## 
## Attaching package: 'lme4'
## The following object is masked from 'package:nlme':
## 
##     lmList
m2lmer <- lmer(
  lang ~ IQ + GS +  SES + COMB + (1 | class), # Fit a separate intercept for each level of class
  data = nlschools
)

summary(m2lmer)
## Linear mixed model fit by REML ['lmerMod']
## Formula: lang ~ IQ + GS + SES + COMB + (1 | class)
##    Data: nlschools
## 
## REML criterion at convergence: 15132.9
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.9588 -0.6488  0.0486  0.7204  3.0765 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  class    (Intercept)  8.507   2.917   
##  Residual             39.998   6.324   
## Number of obs: 2287, groups:  class, 133
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept) 10.63524    1.50012   7.090
## IQ           2.24696    0.07133  31.502
## GS          -0.01562    0.04770  -0.327
## SES          0.16538    0.01479  11.185
## COMB1       -2.02161    0.60055  -3.366
## 
## Correlation of Fixed Effects:
##       (Intr) IQ     GS     SES   
## IQ    -0.484                     
## GS    -0.798 -0.002              
## SES   -0.062 -0.292 -0.057       
## COMB1 -0.168  0.033 -0.006  0.017

Exercises

  • Are the model fits from bayesx() and from lmer() similar?

  • What are the relative sizes of the variances estimated in the random effect term for class versus the residual variance? Does this make sense looking at the boxplot graph above?

Generalised Linear Mixed Models

Mixed effects models can also be considered within the context of generalised linear models. In this case, the linear predictor of observation ii, ηi\eta_i, can be defined as

ηi=Xijβ+ϕi \eta_i = X_{ij}\beta +\phi_i

Compared to the previous setting of linear mixed effects models, note that now the distribution of the response could be other than Gaussian and that observations are not necessarily nested within groups.

Poisson regression

In this practical we will use the North Carolina Sudden Infant Death Syndrome (SIDS) data set. It is available in the spData package and it can be loaded using:

library(spData)
data(nc.sids)
summary(nc.sids)
##     CNTY.ID         BIR74           SID74          NWBIR74      
##  Min.   :1825   Min.   :  248   Min.   : 0.00   Min.   :   1.0  
##  1st Qu.:1902   1st Qu.: 1077   1st Qu.: 2.00   1st Qu.: 190.0  
##  Median :1982   Median : 2180   Median : 4.00   Median : 697.5  
##  Mean   :1986   Mean   : 3300   Mean   : 6.67   Mean   :1051.0  
##  3rd Qu.:2067   3rd Qu.: 3936   3rd Qu.: 8.25   3rd Qu.:1168.5  
##  Max.   :2241   Max.   :21588   Max.   :44.00   Max.   :8027.0  
##      BIR79           SID79          NWBIR79             east      
##  Min.   :  319   Min.   : 0.00   Min.   :    3.0   Min.   : 19.0  
##  1st Qu.: 1336   1st Qu.: 2.00   1st Qu.:  250.5   1st Qu.:178.8  
##  Median : 2636   Median : 5.00   Median :  874.5   Median :285.0  
##  Mean   : 4224   Mean   : 8.36   Mean   : 1352.8   Mean   :271.3  
##  3rd Qu.: 4889   3rd Qu.:10.25   3rd Qu.: 1406.8   3rd Qu.:361.2  
##  Max.   :30757   Max.   :57.00   Max.   :11631.0   Max.   :482.0  
##      north             x                 y             lon        
##  Min.   :  6.0   Min.   :-328.04   Min.   :3757   Min.   :-84.08  
##  1st Qu.: 97.0   1st Qu.: -60.55   1st Qu.:3920   1st Qu.:-81.20  
##  Median :125.5   Median : 114.38   Median :3963   Median :-79.26  
##  Mean   :122.1   Mean   :  91.46   Mean   :3953   Mean   :-79.51  
##  3rd Qu.:151.5   3rd Qu.: 240.03   3rd Qu.:4000   3rd Qu.:-77.87  
##  Max.   :182.0   Max.   : 439.65   Max.   :4060   Max.   :-75.67  
##       lat             L.id           M.id     
##  Min.   :33.92   Min.   :1.00   Min.   :1.00  
##  1st Qu.:35.26   1st Qu.:1.00   1st Qu.:2.00  
##  Median :35.68   Median :2.00   Median :3.00  
##  Mean   :35.62   Mean   :2.12   Mean   :2.67  
##  3rd Qu.:36.05   3rd Qu.:3.00   3rd Qu.:3.25  
##  Max.   :36.52   Max.   :4.00   Max.   :4.00

A full description of the data set is provided in the associated manual page (check with ?nc.sids) but in this practical we will only consider these variables:

  • BIR74, number of births (1974-78).

  • SID74, number of SID deaths (1974-78).

  • NWBIR74, number of non-white births (1974-78).

These variables are measured at the county level in North Carolina, of which there are 100.

Because SID74 records the number of SID deaths, the model is Poisson:

Oi∣μi∼Po(μi),i=1,…,100 O_i \mid \mu_i \sim Po(\mu_i),\ i=1,\ldots, 100 Here, OiO_i represents the number of cases in county ii and μi\mu_i the mean. In addition, mean μi\mu_i will be written as μi=Eiθi\mu_i = E_i \theta_i, where EiE_i is the expected number of cases and θi\theta_i the relative risk in county ii.

The relative risk θi\theta_i is often modelled, on the log-scale, to be equal to a linear predictor:

log(θi)=β0+… \log(\theta_i) = \beta_0 + \ldots

The expected number of cases is computed by multiplying the number of births in county ii to the overall mortality rate

r=∑i=1100Oi∑i=1100Bi r = \frac{\sum_{i=1}^{100}O_i}{\sum_{i=1}^{100}B_i} where BiB_i represents the total number of births in country ii. Hence, the expected number of cases in county ii is Ei=rBiE_i = r B_i.

# Overall mortality rate
r74 <- sum(nc.sids$SID74) / sum(nc.sids$BIR74)
# Expected cases
nc.sids$EXP74 <- r74 * nc.sids$BIR74

A common measure of relative risk is the standardised mortality ratio (Oi/EiO_i / E_i):

nc.sids$SMR74 <- nc.sids$SID74 / nc.sids$EXP74

A summary of the SMR can be obtained:

hist(nc.sids$SMR, xlab = "SMR")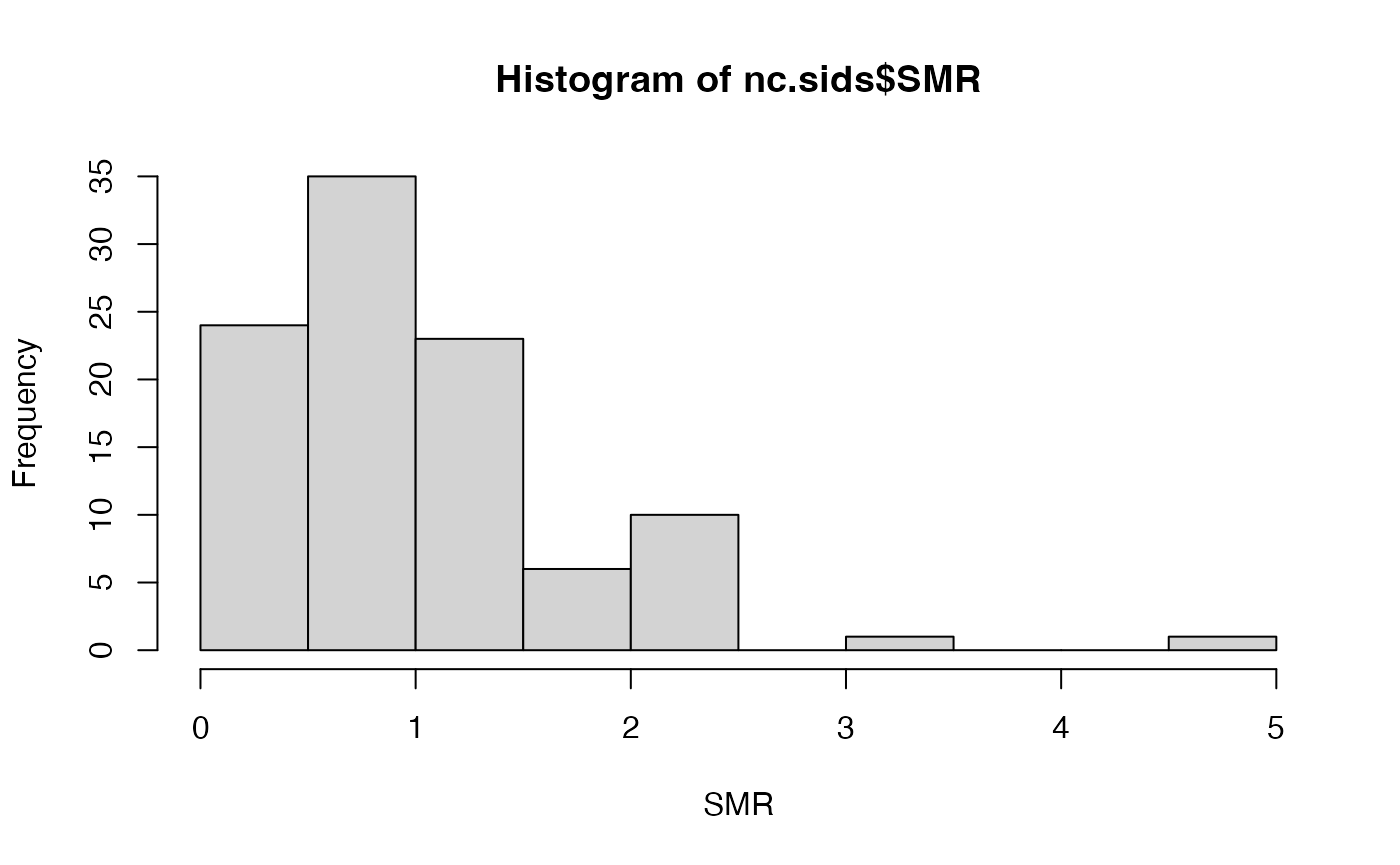

Values above 1 indicate that the county has more observed deaths than expected and that there might be an increased risk in the area.

As a covariate, we will compute the proportion of non-white births:

nc.sids$NWPROP74 <- nc.sids$NWBIR74/ nc.sids$BIR74

There is a clear relationship between the SMR and the proportion of non-white births in a county:

plot(nc.sids$NWPROP74, nc.sids$SMR74)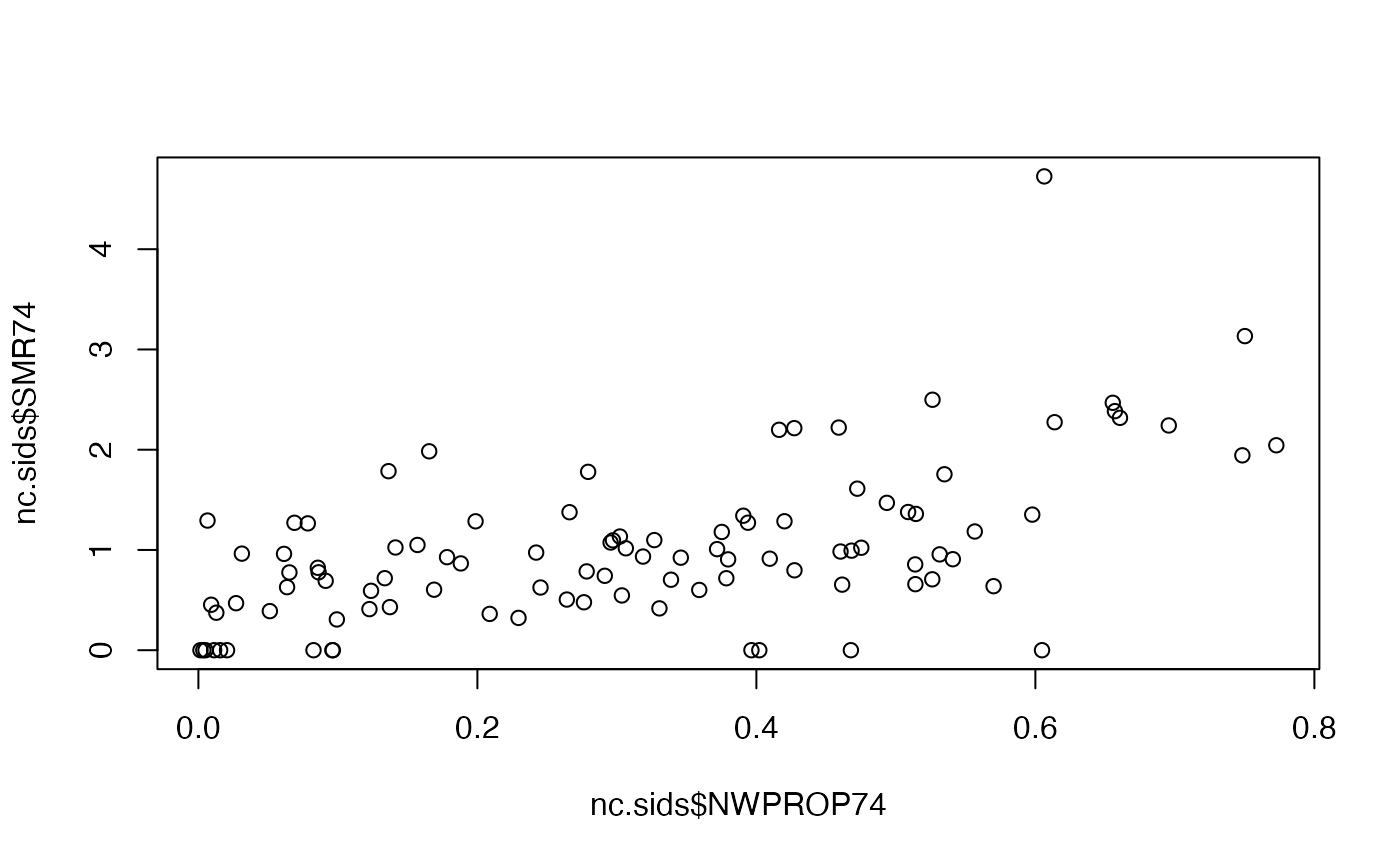

# Correlation
cor(nc.sids$NWPROP74, nc.sids$SMR74)
## [1] 0.5793901

A simple Poisson regression can be fit by using the following code:

m1nc <- bayesx(
  SID74 ~ 1 + NWPROP74,
  family = "poisson",
  offset = log(nc.sids$EXP74),
  data = nc.sids
)
summary(m1nc)
## Call:
## bayesx(formula = SID74 ~ 1 + NWPROP74, data = nc.sids, offset = log(nc.sids$EXP74), 
##     family = "poisson")
##  
## Fixed effects estimation results:
## 
## Parametric coefficients:
##                Mean      Sd    2.5%     50%   97.5%
## (Intercept) -0.6463  0.0906 -0.8189 -0.6458 -0.4542
## NWPROP74     1.8710  0.2206  1.4250  1.8681  2.3064
##  
## N = 100  burnin = 2000  method = MCMC  family = poisson  
## iterations = 12000  step = 10

Random effects can also be included to account for intrinsic differences between the counties:

# Index for random effects
nc.sids$ID <- 1:nrow(nc.sids)

# Model WITH covariate
m2nc <- bayesx(
  SID74 ~  1 + NWPROP74 + sx(ID, bs = "re"),
  family = "poisson",
  offset = log(nc.sids$EXP74),
  data = as.data.frame(nc.sids)
)

summary(m2nc)
## Call:
## bayesx(formula = SID74 ~ 1 + NWPROP74 + sx(ID, bs = "re"), data = as.data.frame(nc.sids), 
##     offset = log(nc.sids$EXP74), family = "poisson")
##  
## Fixed effects estimation results:
## 
## Parametric coefficients:
##                Mean      Sd    2.5%     50%   97.5%
## (Intercept) -0.6617  0.1067 -0.8720 -0.6661 -0.4590
## NWPROP74     1.9076  0.2624  1.3904  1.9105  2.4407
##  
## Random effects variances:
##             Mean     Sd   2.5%    50%  97.5%    Min    Max
## sx(ID):re 0.0571 0.0298 0.0059 0.0551 0.1210 0.0012 0.1709
##  
## N = 100  burnin = 2000  method = MCMC  family = poisson  
## iterations = 12000  step = 10

We can see the fitted relationship with NWPROP74:

x.predict <- seq(0,1,length=1000)
y.predict <- exp(coef(m2nc)["(Intercept)","Mean"]+coef(m2nc)["NWPROP74","Mean"]*x.predict)
par(mfrow = c(1, 1))
plot(nc.sids$NWPROP74, nc.sids$SMR74)
lines(x.predict,y.predict)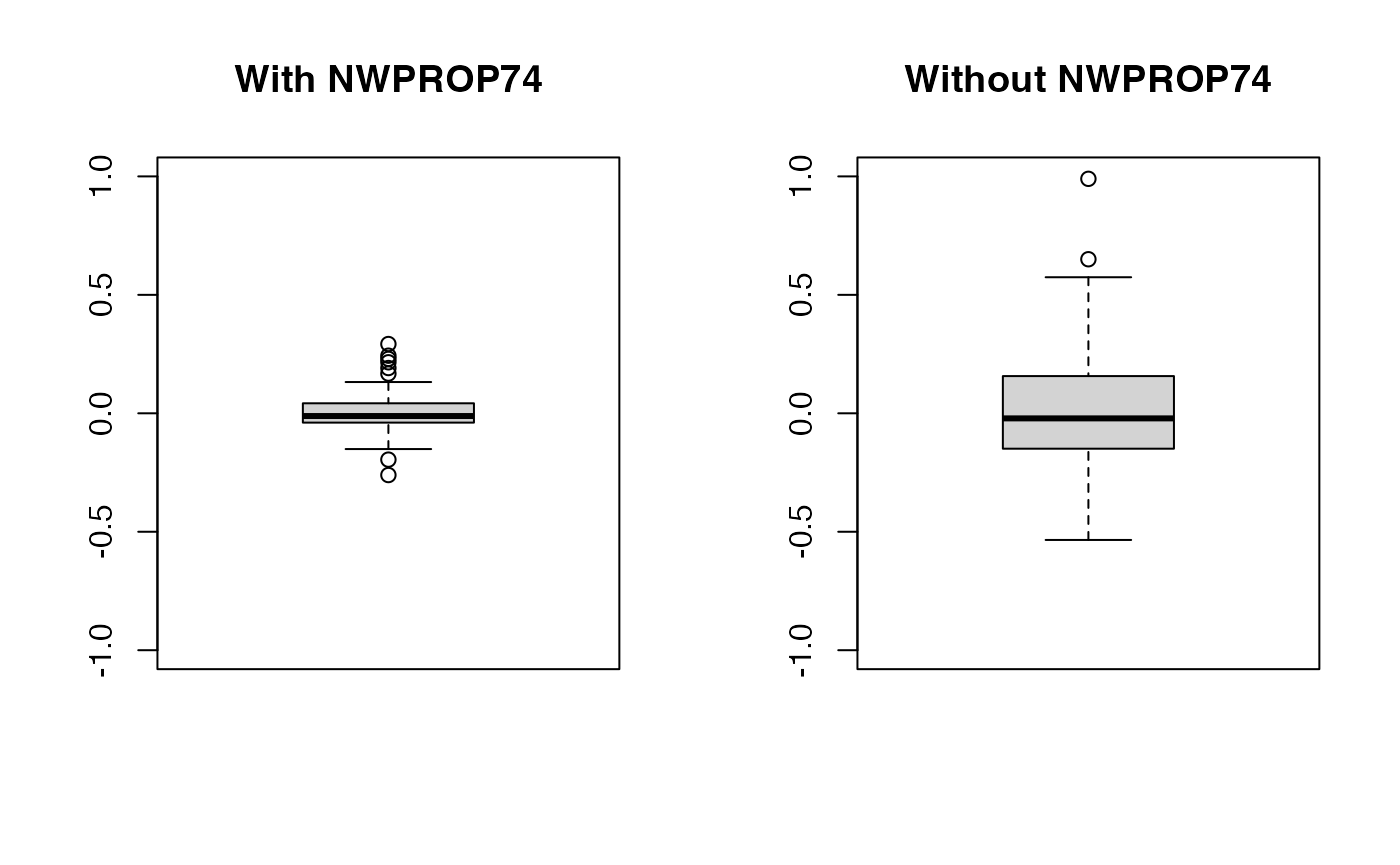

The role of the covariate can be explored by fitting a model without it:

# Model WITHOUT covariate
m3nc <- bayesx(
  SID74 ~  1 + sx(ID, bs = "re"),
  family = "poisson",
  offset = log(nc.sids$EXP74),
  data = as.data.frame(nc.sids)
)

summary(m3nc)
## Call:
## bayesx(formula = SID74 ~ 1 + sx(ID, bs = "re"), data = as.data.frame(nc.sids), 
##     offset = log(nc.sids$EXP74), family = "poisson")
##  
## Fixed effects estimation results:
## 
## Parametric coefficients:
##                Mean      Sd    2.5%     50%  97.5%
## (Intercept) -0.0317  0.0651 -0.1665 -0.0298 0.0864
##  
## Random effects variances:
##             Mean     Sd   2.5%    50%  97.5%    Min    Max
## sx(ID):re 0.1743 0.0530 0.0914 0.1680 0.2973 0.0454 0.3867
##  
## N = 100  burnin = 2000  method = MCMC  family = poisson  
## iterations = 12000  step = 10

Now, notice the decrease in the estimate of the precision of the random effects (i.e., the variance increases). This means that values of the random effects are now larger than in the previous case as the random effects pick some of the effect explained by the covariate.

par(mfrow = c(1, 2))
boxplot(m2nc$effects$`sx(ID):re`$Mean, ylim = c(-1, 1), main = "With NWPROP74")
boxplot(m3nc$effects$`sx(ID):re`$Mean, ylim = c(-1, 1), main = "Without NWPROP74")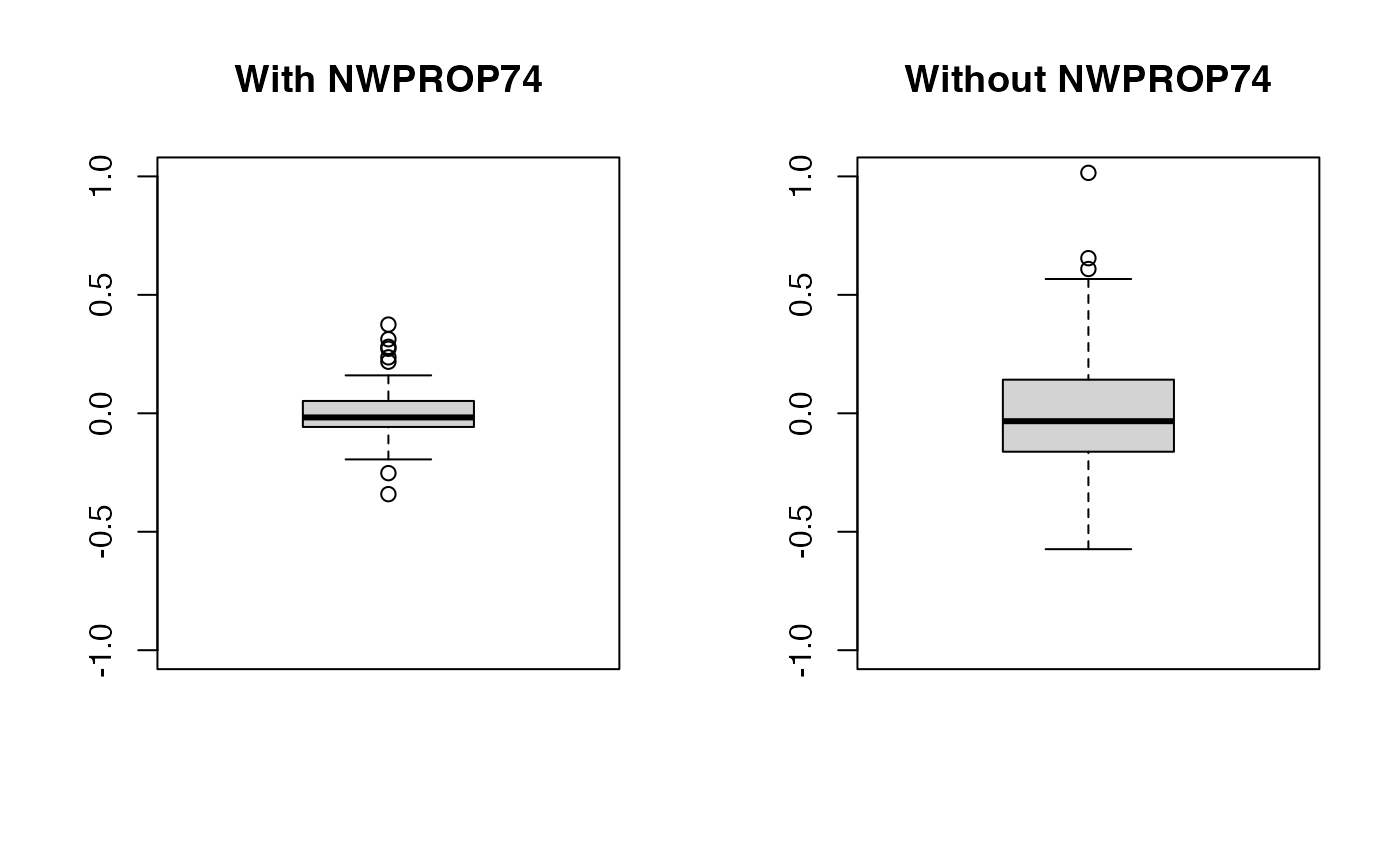

Further Extensions

Spatial random effects can be defined not to be independent and identically distributed. Instead, spatial or temporal correlation can be considered when defining them. For example, in the North Carolina SIDS data set, it is common to consider that two counties that are neighbours (i.e., share a boundary) will have similar relative risks. This can be taken into account in the model but assuming that the random effects are spatially autocorrelated. This is out of the scope of this introductory course but feel free to ask about this!!

Final Exercises (Optional!!)

We tend to use the final Practical session for catching up and to give you the opportunity to ask us any questions you may have. So please ask away!

If you would like some further exercises to practice, please look at Practical 8 for more material and examples, including the use of the non-MCMC package INLA.